| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- gptapi
- nvmrc
- nodejs
- git
- gitlab
- Github
- class
- 웹소켓재시작
- gpt3.5turbo
- 자바
- aiapi
- 노드버전
- 클래스
- 패키지설치에러
- 호스팅영역
- 버킷생성
- javascript
- java
- GPT3.5
- Database
- 웹소켓연결끊김
- db
- openaiapi
- iam사용자
- 클라우드
- 웹소켓연결
- aws
- Express
- ChatGPT
- chatGPTAPI
- Today
- Total
IT's Jenna
10. 그래프에 맞서다 본문
그래프란?
그래프의 종류
SQL과 그래프
그래프에 대한 쿼리
트리
RDB에서 그래프를 다루기는 매우 어렵습니다. 이전장에서 설명한 이력 데이터와 마찬가지로 그래프는 관계형 모델로 표현하기 굉장히 어려운 구조로 되어있죠. 하지만 늘 그렇듯이 우리는 방법을 찾아야 하고 이번장에서는 그 방법들을 설명해보도록 하겠습니다.
그래프란?
우선 그래프란 무엇인지를 먼저 알아야겠죠? 그래프란 노드와 에지 두 가지 요소를 이용해서 사건의 관련성등을 표현할 수 있는 수학적인 데이터 구조를 의미합니다. 그래프는 여러 개의 노드가 에지로 연결된 구조로 되어 있습니다.
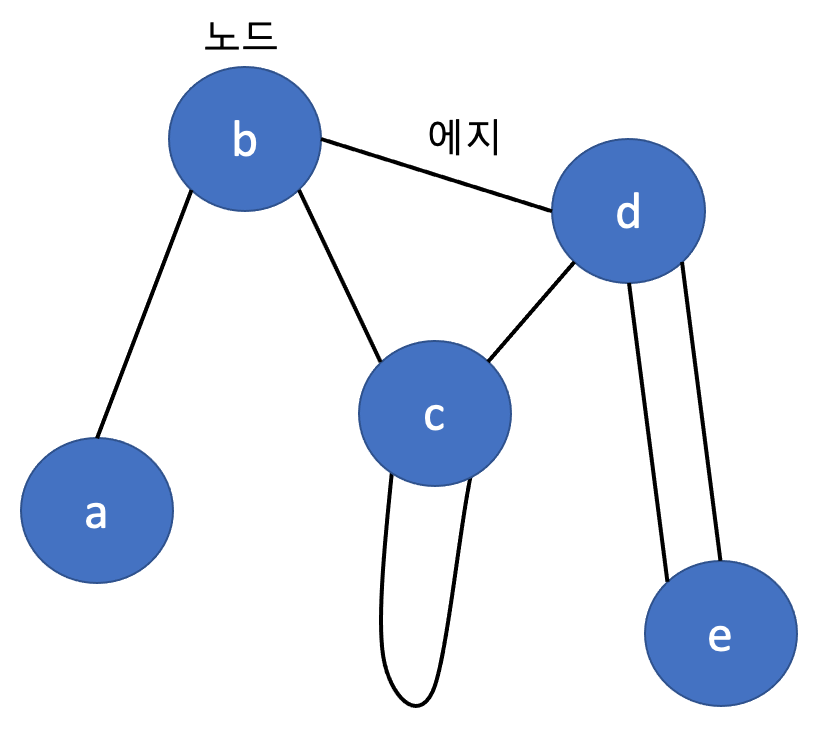
위 그림에서 노드 a와 b를 연결하는 에지를 ab라고 표현합니다. 그래프는 다양한 성질을 가질 수 있는데 각각에 대해서 한번 알아봅시다!
1. 인접
노드와 노드사이가 에지로 연결되어 있으면 두 노드는 인접하고 있다. 또는 연결이라고 표현합니다.
2. 차수
어떤 노드에 연결된 에지의 수를 차수라고 합니다. 위 그림에는 차수가 1~4인 노드들이 존재합니다.
3. 보행,트레일,길
어떤 노드에서 다른 노드에 이르는 길을 보행(walk)라고 합니다. a노드에서 c노드로 가는 (ab, bd, db, bd, db, bc)는 보행입니다. 보행은 노드와 에지를 중복해서 지나도 괜찮습니다.
이때 같은 에지를 두 번 통과하지 않는 것을 트레일(trail)이라고 합니다. 그리고 같은 노드를 두번 통과하지 않는것을 길(path) 또는 경로라고 합니다.
4. 다중 에지
두 노드 간에 여러 개의 에지가 있는 경우 다중 에지라고 합니다. 위에서 두 개의 de에지가 다중 에지입니다. 이런 경우엔 에지를 구분하기 위해 에지 자체에 라벨을 붙여서 식별합니다.
5. 루프
노드가 자기 자신과 연결된 에지를 루프라고 합니다. 루프는 여러 번 통과해도 결국 같은 노드에 도달합니다.
6. 닫힌 보행
어떤 노드에서 시작해서 같은 노드로 돌아오는 경로를 닫힌 보행이라고 합니다. 루프와 다중 에지를 가진 두 개의 노드도 닫힌 보행의 일종입니다. 이때 처음과 시작 노드만 두 번 통과할 수 있고 사이 경로 상에서는 노드 중복은 불가합니다.
7. 연결
그래프 상 모든 노드 사이이에 경로가 존재할 때 그 그래프는 연결되어 있다고 합니다.
8. 부분 그래프
그래프에서 임의의 에지나 노드를 제거할 때 생기는 그래프를 부분 그래프라고 합니다.
9. 컷 세트, 브리지
도달할 수 없는 노드가 있는 그래프를 비연결 그래프라고 합니다. 이때 어떤 에지를 제거해도 비연결 그래프가 되지 않는 에지들을 컷 세트라고 합니다. 위의 예시에서 {bd, bc}는 컷 세트입니다.
노드 간 연결되는 에지가 하나뿐인 경우에 이것을 브릿지라고 합니다. 위의 예시에서 {ab}가 브리지입니다.
10. 에지의 방향과 가중치
그래프의 에지에 방향과 가중치를 붙일 수도 있습니다.
이렇게 그래프에는 다양한 성질이 존재합니다. 그렇다면 이러한 그래프는 어떻게 활용이 될까요? 아래 그래프가 사용되는 구체적인 예시들이 있습니다.
- 소셜 네트워크
- 웹 페이지 링크
- 전자회로
- 네트워크 다이어그램
- 화학식
- 노선도
- 조직도
- 부품표(BOM)
- 게시판
- 파일 시스템
그래프의 종류
위에서 언급한 그래프들의 성질에 따라 그래프 종류를 나눌 수 있습니다.
1. 일반 그래프
어떠한 제한도 없는 그래프를 일반 그래프 또는 그래프라고 합니다. 자유도가 높고 법칙이 정해져 있지 않아서 다루기가 어렵습니다. 위의 예시가 일반 그래프입니다.
2. 단순 그래프
다중 에지 및 루프가 없는 그래프를 단순 그래프라고 합니다. 일반 그래프보다 다루기 쉬워 일반적으로 단순 그래프를 이용하다가 일반 그래프로 확장해나가는 방식으로 사용합니다.

3. 연결 그래프/비연결 그래프
위의 예시들에서는 임의의 두 노드 간에 경로가 있었습니다. 이러한 그래프를 연결 그래프라고 합니다. 반대로 노드간에 도달할 수 있는 경로가 없을 때 비연결 그래프라고 합니다. 일반적으로 연결 그래프가 다루기 쉽습니다.

4. 완전 그래프
단순 그래프 중 모든 노드가 서로 인접해있는 그래프를 완전 그래프라고 합니다. 노드 수 n에 대해 각각 n-1개의 노드와 인접하므로 완전 그래프의 총 에지수는 정확히 n(n-1)/2개입니다.
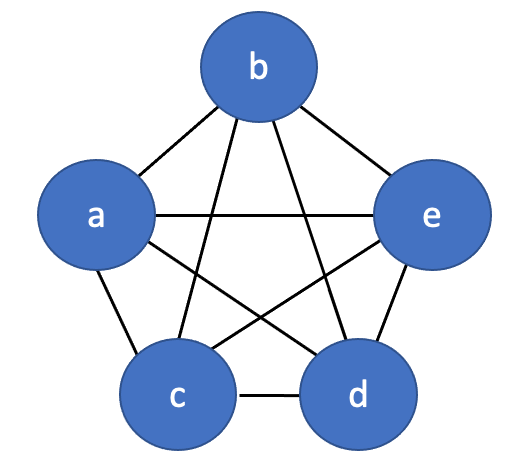
5. 정규 그래프
모든 노드의 차수가 같은 그래프를 정규 그래프라고 합니다. 완전 그래프로 정규 그래프입니다.
6. 평면 그래프
어떤 에지도 교차하지 않는 그래프를 평면 그래프라고 합니다. 에지가 교차하지 않기 때문에 평면상에 기술할 수 있다는 의미에서 평면 그래프라고 이름 붙여졌습니다. 예시로 회로 기판이 평면 그래프의 일종입니다.
7. 유향 그래프/무향 그래프
에지의 연결이 단방향이면 유향 그래프, 방향이 정해져 있지 않으면 무향 그래프라고 합니다. 위의 예시들은 모두 무향 그래프였습니다. 방향을 사용할지 여부는 그 그래프로 어떤 것을 표현할 것인지에 따라 달라집니다. 예를 들어 도로를 모델화 하는 경우 일방통행을 생각해서 유향 그래프를 이용해야 합니다.
8. 가중 그래프
에지에 가중치를 부여해 노드 사이의 거리나 도달 시간 등을 표시하고 그에 따른 비용을 계산하는 모델을 표현할 수 있습니다. 이것을 가중 그래프라고 합니다. 최단 경로 탐색 또는 처리량 계산할 때 가중 그래프가 사용됩니다.
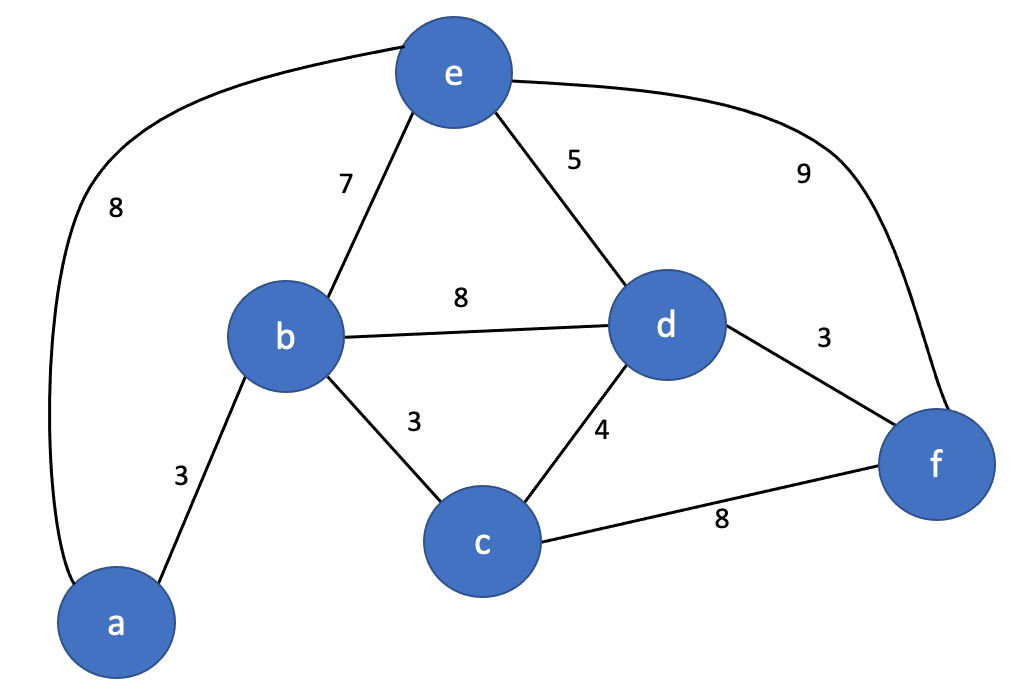
9. 트리
트리구조는 데이터를 표현할 때에 많이 사용됩니다. 트리는 단순 그래프 중에서 가장 단순한 구조로 되어 있는 그래프입니다. 이러한 단순한 특성 때문에 트리에서만 적용될 수 있는 다양한 기법이 존재합니다. 트리에 대해서는 이후에 더 자세히 설명하도록 하겠습니다.
SQL과 그래프
데이터를 저장만 하기 위해서는 그래프를 관계형 모델로 표현하는 것은 매우 간단합니다. 이런 경우엔 노드의 집합과 에지의 다중 집합을 각각 저장하면 됩니다. 이와 같은 모델을 인접 리스트 모델이라고 합니다.
그런데 여기서 문제는 쿼리입니다. DB에서 필요한 데이터를 얻기 위해서 쿼리를 사용하는데 단순한 인접 리스트에서는 쿼리문을 활용해서 모든 데이터를 얻을 수 없습니다.
그래프에 사용되는 쿼리의 예시들은 다음과 같습니다.
- 어떤 노드 A에서 다른 노드 B로 경로가 존재하는가?
- 경로가 존재한다면 최단 경로는 무엇인가?
- 그래프는 평면인가?
- 그래프에 닫힌 보행이 있는가?
- 모든 에지를 한 번씩 통과하고 원래의 노드로 돌아오는 트레일이 존재하는가?
- 원래의 노드로 돌아오지 않지만 모든 에지를 한번씩 통과하는 트레일이 존재하는가?
- 모든 노드를 통과하고 원래의 노드에 돌아오는 최단 경로는 어떤 것인가?
인접 리스트를 통해서는 위의 질의에 대한 답을 도출할 수 없습니다.
예를 들어 위의 가중 그래프에서 <a에서 f에 이르는 최단 경로는 어떤 것인가?>라는 질의가 있다고 생각해봅시다. 이를 위해 우선 그래프를 RDB에 인접 리스트로 표현하면 다음과 같습니다.

과연 위 DB설계는 잘 표현된 것일까요? 아닙니다. 사실상 에지는 하나의 단위로 되어 있는 것이기 때문에 하나의 칼럼으로 표현되어야 합니다. ab라는 두 개의 요소가 하나의 칼럼 값으로 표현되는 것이 올바른 표현 방법인 것이죠. 결국 RDB에서는 무향 그래프를 제대로 표현할 수 없습니다.
그렇다면 유향 그래프를 생각해 볼까요? 유향 그래프라면 에지의 시작점과 끝점을 start_node, end_node로 표현할 수 있습니다. 위의 가중 그래프가 전이중 유향 그래프라고 가정하고 그에 대한 RDB를 작성해보면 다음과 같습니다.

사실상 무향 그래프를 유향 그래프로 표현하는 것은 기존에 의도했던 것과는 다른 모델이 된 것입니다. 즉, 쿼리를 작성하기 위해서 알고리즘에 변화를 주는 주객전도의 형태가 된 것이죠. 하지만 알고리즘을 변경해도 일치하는 경과를 얻을 수 있다면 결국 문제는 없습니다. 따라서 신중할 필요는 있지만 모델을 바꾸는 방법도 필요할 땐 사용되어야 합니다.
그래프에 대한 쿼리
그렇다면 이제 그래프를 표현한 테이블에서 사용할 수 있는 쿼리문을 알아봅시다. <a에서 f에 이르는 최단 경로는 어떤 것인가?>라는 쿼리는 어떻게 작성할까요?
우선 노드 a에서 출발해서 n개의 에지를 통과 후 f에 이르는 경로들을 찾아봅시다.
1. a에 인접한 노드 구하기
SELECT end_node
FROM sys.edges_
WHERE start_node = 'a';
2. 자기 결합으로 다음 인접 노드 구하기
SELECT e2.end_node
FROM sys.edges_ e1
JOIN sys.edges_ e2
ON e1.end_node = e2.start_node
WHERE e1.start_node = 'a';
여기서 가장 큰 문제는 JOIN을 몇 번을 실행해야 할지 알 수 없다는 것입니다. end_node가 f라는 조건을 만족할 때까지 처리를 계속하는 것은 루프 또는 분기 처리가 필요합니다. 하지만 이러한 수행방식은 절차형 처리에서 사용 가능한 것이고 선언적 프로그래밍 언어인 sql과는 사용할 수 없습니다.
게다가 weight를 기반한 최단 경로는 사실상 a-b-c-d-f입니다. 노드수가 더 적은 경로는 a-e-f일 수 있겠지만 이것은 사실상 최단 경로는 아닌 것입니다.
결국 관계형 모델은 그래프 탐색이라는 문제를 다루기 어렵습니다. 하지만 이때 sql server에서 제공하는 저장 프로시저라는 기능을 사용하면 함수 형식으로 테이블을 여러 번 조인하거나 조건을 걸어주는 등의 동작을 메서드처럼 만들 수 있습니다. 해당 방법에 대해서는 이번 장에서 다루지는 않겠습니다. 하지만 한번 찾아보시는 것을 추천드립니다!
트리
위에서 언급했던 트리에 대해서 설명해보도록 하겠습니다. 트리는 가장 많이 사용되는 그래프의 한 종류입니다. 그렇다면 트리는 대체 무엇일까요? 아래는 트리의 예시입니다.

아래는 수학적 의미에서의 트리에 대한 조건입니다.
- 트리는 닫힌 보행이 없이 연결돼 있습니다.
- 모든 에지는 브리지입니다.
- 임의의 두 노드를 연결하는 경로는 하나뿐입니다.
- 인접하지 않은 어떤 두 개의 노드를 연결해도 닫힌 보행이 될 수 있습니다.
아래는 모델링에서 트리를 사용할 때에 대한 조건입니다.
- 부모 자식 관계가 있는 유향 그래프입니다.
- 어떤 노드로 향하는 에지는 하나뿐입니다.
- 모든 노드에 출발점이 되는 뿌리(root) 노드가 있습니다.
- 뿌리에서 거리의 깊이로 표현합니다. (계층구조 형식)
그래프를 관계형 모델에서 처리하기는 어렵다고 계속 설명했습니다. 트리도 그래프의 일종이기 때문에 완벽히 처리될 수는 없지만 위의 조건들로 인해서 비교적 쉽게 처리하는 방법을 도출할 수 있었습니다. 지금부터 그 방법들을 알아봅시다!
1. 인접 리스트 모델
트리도 인접 리스트를 이용해서 표현할 수 있습니다. 에지는 부모 방향으로 하나만 있기 때문에 테이블에 parent_id를 주로 포함합니다.

이때 뿌리 노드의 parent_id는 null이 됩니다. 관계형 모델에 있어서 null은 좋지 않다고 말씀드렸지만 트리에서는 이러한 상태가 실질적으로 문제가 되지는 않습니다. 그럼에도 불구하고 null을 포함하지 않는 테이블을 만들고 싶다면 다음과 같이 나타낼 수도 있습니다.

위의 인접 리스트 모델을 이용해서 <노드 f의 계층 깊이는 얼마인가?>를 구하는 쿼리는 다음과 같이 작성할 수 있습니다. 이 외의 그래프에 관한 추가 질의들의 쿼리도 쉽게 작성 가능합니다.
WITH RECURSIVE r AS (
SELECT 1 AS level, node_id, parent_id
FROM sys.tree_
WHERE parent_id IS NULL
UNION ALL
SELECT r.level + 1, t.node_id, t.parent_id
FROM r JOIN sys.tree_ t
ON r.node_id = t.parent_id)
SELECT * FROM r WHERE node_id = 'f';

쿼리의 결과 이해에 도움을 주기 위해서 마지막 WEHRE조건절을 뺀 SELECT * FROM r의 결과 테이블을 덧붙이겠습니다.

2. 경로 열거 모델
각 노드의 루트에서의 경로를 이용해 트리를 표현할 수도 있습니다.

경로 열거 모델은 미리 경로를 포함하고 있기 때문에 노드 사이의 부모 관계를 파악하기 용이합니다. 그렇기 때문에 경로를 검색하기 위한 쿼리 역시 비교적 쉽습니다. 아래는 <b의 자식 노드는 어떤 것인가?>라는 쿼리문입니다.
SELECT * FROM sys.tree_2
WHERE path LIKE CONCAT((
SELECT path
FROM sys.tree_2
WHERE node_id='b'), '%')b의 path인 /a/b로 시작하는 path경로를 가진 것들을 출력하게끔 쿼리문을 작성했습니다. 결과는 다음과 같습니다.
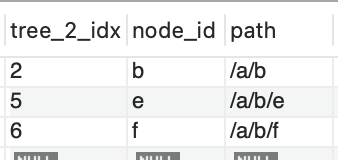
이렇게 LIKE문을 활용하면 경로 열거 모델에서 데이터 검색은 쉽습니다. 하지만 가져온 데이터를 활용할 때는 문제점이 있습니다. 경로의 구분이 /문자로 되어 있기 때문에 데이터를 취득할 때 문자열을 분해하여 노드 정보를 추출해야 합니다.
3. 클로저 테이블
클로저 테이블은 모든 노드에 '노드 x는 노드 y의 부모이다'라는 개념으로 저장한 테이블입니다. 위의 트리를 클로저 테이블로 표현하면 다음과 같습니다.

클로저 테이블은 모든 노드 정보를 저장하기 때문에 테이블의 크기가 매우 크다는 단점이 있습니다. 하지만 관계형 모델에 대한 친화성을 가장 높다는 것이 특징입니다!
클로저 테이블에 대한 질의 간 가장 간단하고 활용하기 용이합니다. 예를 들어 'C의 자식은 어느 것인가?'라는 질의에 대한 쿼리문은 다음과 같습니다.
SELECT descendant FROM sys.tree_closure
WHERE ancestor = 'c';또한 g의 깊이를 구하는 쿼리는 아래와 같습니다.
SELECT COUNT(1) FROM sys.tree_closure WHERE descendant = 'g'결과적으로 트리를 RDB 상에서 표현할 때 가장 추천하는 방식은 클로저 테이블입니다. 그다음으로는 구조가 단순한 인접 리스트 모델을 추천합니다. 하지만 결국 그래프는 관계형 모델에는 없는 개념이므로 RDB에서 다루기 쉽지 않은 것은 사실입니다. 어떠한 방법도 절대적인 해답이 아니기 때문에 그때그때 상황에 맞게 활용할 수 있어야 할 것입니다.
'Study > 관계형 데이터 베이스 실전 입문' 카테고리의 다른 글
| 9. 이력 데이터와 친해지기 (0) | 2021.06.28 |
|---|---|
| 8. SELECT를 공략하자 (0) | 2021.06.02 |
| 7. NULL과의 싸움 (0) | 2021.06.01 |
| 6. 도메인 설계 전략 (0) | 2021.05.28 |
| 5. 릴레이션의 직교성 (0) | 2021.05.27 |




